The Three-Body Problem has been a subject of fascination and frustration for scientists and mathematicians for centuries, encapsulating the unpredictable complexity that arises when three celestial bodies, like stars or planets, interact with each other gravitationally. In a universe where the gravitational ballet between two bodies can be elegantly described by Newton’s laws, introducing a third body complicates this dance to an extent that defies straightforward prediction. This problem, which seems simple at its core, asks how three bodies will move under the influence of gravity, based on their initial positions and velocities. Its significance lies not just in theoretical physics but also in its practical implications for understanding the cosmos, from the motion of planets in our solar system to the dynamics of distant star systems.
When two bodies are involved, their gravitational interaction leads to predictable orbits, as beautifully demonstrated by the Earth’s journey around the Sun. This predictable nature stems from the precise mathematical solutions to Newton’s equations of motion, which elegantly describe the paths these bodies will follow. However, add another body into this mix, and predictability fades into chaos. The Three-Body Problem is notorious for its lack of a general solution, meaning there is no single mathematical formula that can predict the motions of all three bodies in every possible scenario. The challenge arises because the gravitational influence between each pair of bodies must be considered, and as they move, these influences constantly change in a non-linear fashion, leading to a situation where small differences in initial conditions can drastically alter the outcome.
The history of the Three-Body Problem is marked by significant milestones, notably including Henri Poincaré’s late 19th-century work, which unveiled the problem’s inherent unpredictability and sensitivity to initial conditions—a key aspect of what is today known as chaos theory. Poincaré’s insights laid the foundation for modern dynamics and showed that even deterministic systems, governed by precise laws, can exhibit unpredictable behavior. This revelation was profound, suggesting that the universe’s deterministic laws do not always lead to predictable outcomes, a notion that challenges our understanding of the natural world.
Transitioning to the more technical and mathematical aspect, the Three-Body Problem is encapsulated in a set of differential equations derived from Newton’s laws of motion and his law of universal gravitation. These equations account for the gravitational forces acting between each pair of bodies, leading to a complex system of equations that are highly non-linear and interdependent. The non-linearity arises from the equations’ dependence on the inverse square of the distance between the bodies, a relationship that ensures the forces and therefore the motions become intricately linked in a manner that defies simple analytical solutions.
In the realm of celestial mechanics, solutions to the Two-Body Problem are well-established, providing precise orbits and paths for the bodies involved. However, with the addition of a third body, the system’s dynamics become chaotic, making long-term predictions nearly impossible. This chaos is characterized by an extreme sensitivity to initial conditions, a hallmark of chaotic systems, where minuscule variations in the starting positions or velocities can lead to vastly different trajectories over time.
Mathematically, the Three-Body Problem involves solving a series of differential equations that describe the motion of the bodies based on the forces they exert on each other. For bodies with masses

and positions represented by vectors

the goal is to determine the motion of each body over time. The gravitational force experienced by each body is the sum of the forces exerted by the other two, leading to a set of equations that must be solved simultaneously to predict the system’s evolution.
Despite the problem’s complexity, certain specific solutions and approximations have been discovered. For example, the Lagrange points represent scenarios where the gravitational forces and the orbital motions of the bodies balance, allowing for stable configurations. However, these solutions are exceptions rather than the rule, and the general Three-Body Problem remains unsolved in the sense of finding a universal analytical solution. In practice, numerical simulation has become a powerful tool for approximating the future states of three-body systems, allowing scientists to explore the dynamics of such systems with incredible detail, albeit without the elegance and generality of a closed-form solution.

The Three-Body Problem, central to celestial mechanics, concerns the motion of three celestial bodies under their mutual gravitational attraction. Rooted in Newton’s law of universal gravitation, which posits that the force between two masses is directly proportional to the product of their masses and inversely proportional to the square of the distance between them

where F is the gravitational force, G is the gravitational constant, m1 and m2 are the masses, and r is the distance between the masses. The complexity arises when applying Newton’s second law, F = ma, leading to a set of nonlinear differential equations governing the bodies’ motions:
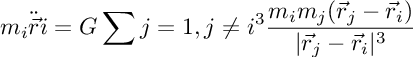
with mi and mj being the masses,

the position vectors, and

the acceleration vector for each body. The difficulty in finding a general analytical solution lies in these equations’ sensitivity to initial conditions and inherent non-linearity, often leading to chaotic trajectories that defy simple prediction.
Despite this, the problem admits specific solutions under certain symmetries and initial conditions. Lagrange and Euler found solutions where bodies maintain relative equilibrium positions or align linearly, respectively. The restricted Three-Body Problem, considering a negligible mass third body, yields insights into periodic orbits and quasi-periodic solutions under particular scenarios. However, for arbitrary initial conditions, the system’s behavior is predominantly studied through numerical simulations, discretizing time to approximate the bodies’ paths over intervals. This approach, while lacking the elegance of closed-form solutions, offers pragmatic insights into system dynamics, informing spacecraft trajectory design and deepening our understanding of celestial mechanics. Advanced mathematical techniques, including perturbation methods, symplectic integrators, and chaos theory, have further enriched our grasp of the problem, illustrating the intricate dance of celestial bodies through both deterministic laws and unpredictable outcomes. The Three-Body Problem thus remains a cornerstone of mathematical and physical inquiry, embodying the interplay between order and chaos inherent in the universe’s fabric.
All images and all text in this blog were created by artificial intelligences

